
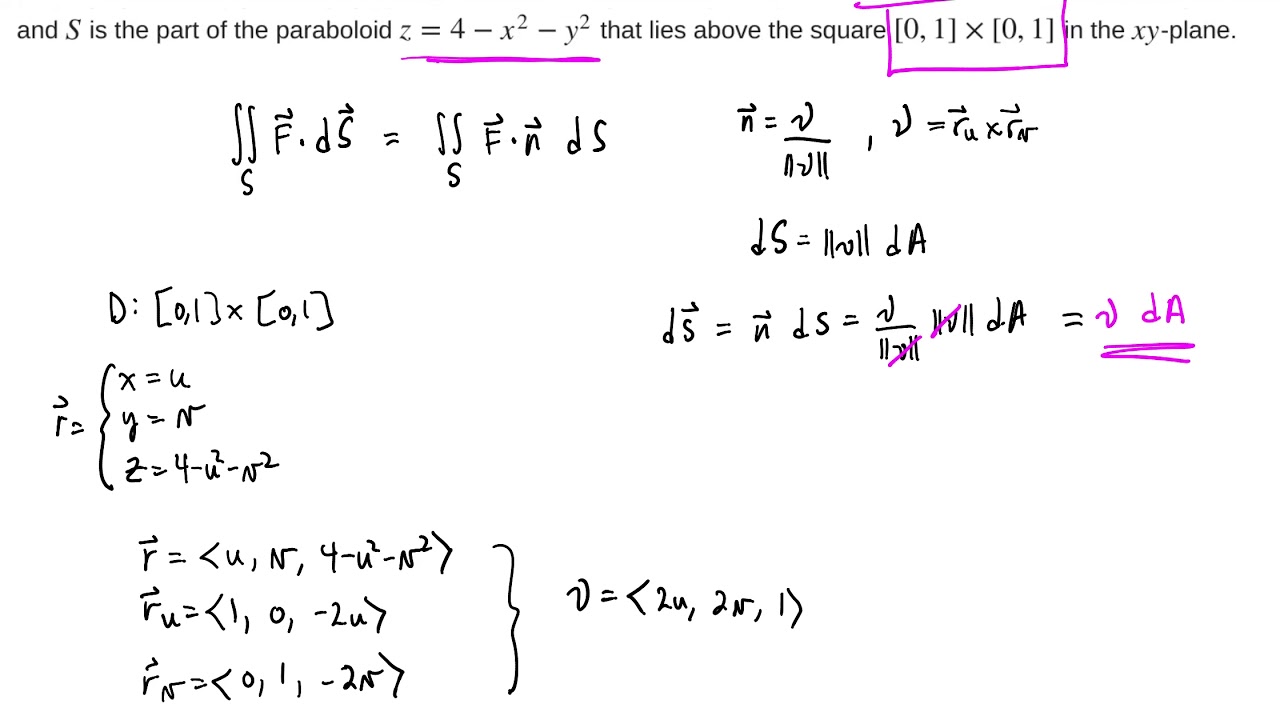
The luminous flux is found from the spectral flux and the V() function from the following relationship: luminousflux 683 ( ) ( ).

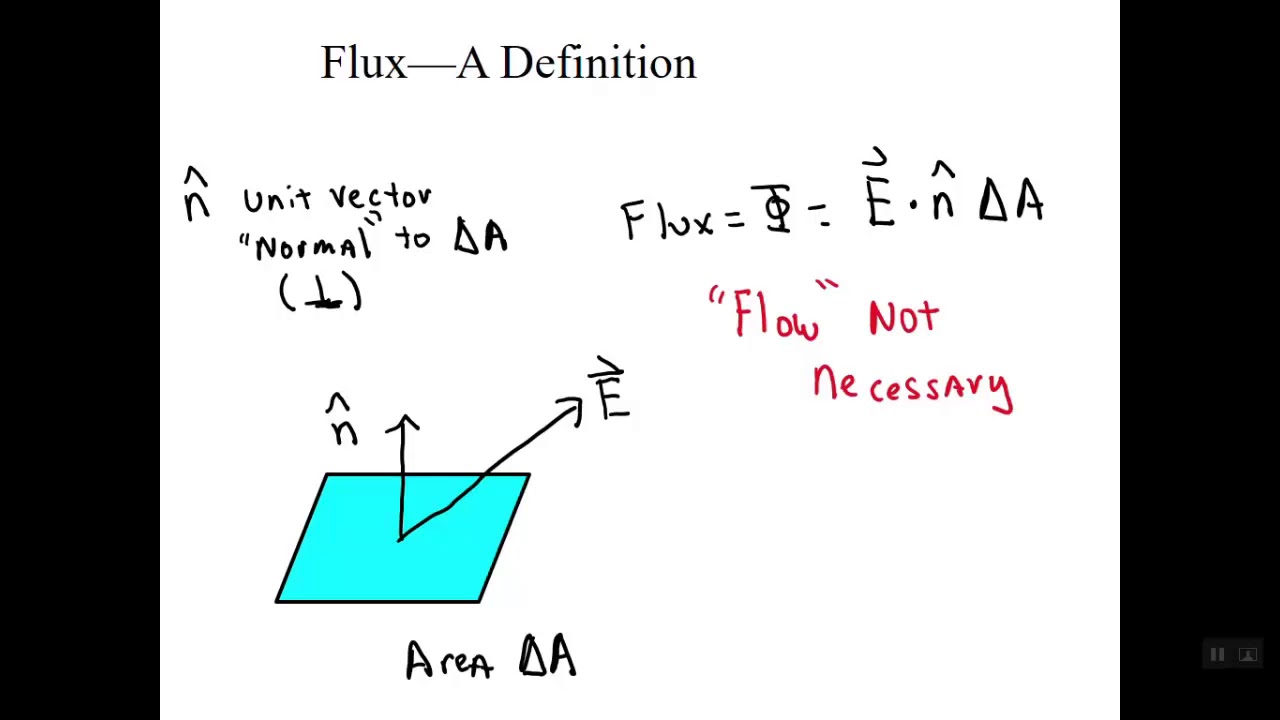
Don't worry, you'll see what I mean in the next article. The flux (or surface integral) of a vector field F through the surface > of normal unit vector N and area element dS is JL F NdS Definition 2.16. The unit of luminous (photopic) flux is the lumen. Please fix it on your own.ġ.) “Normalize” dataset - 0 instead of negative values: SELECT MEAN(value) AS meanĢ.) Next step add integral (+ some math will be required as well to have proper Wh value - pls develop it on your own) SELECT INTEGRAL("mean", 5m) AS integralģ.∮ C F ⋅ n ^ d s = ∫ 0 2 π F ( r ( t ) ) ⋅ ⏟ Velocity at a point n ^ ( r ( t ) ) ⏞ Normal vector at a point ∣ ∣ r ′ ( t ) ∣ ∣ d t ⏟ d s = ∫ 0 2 π ( ⋅ ) ∣ ∣ ∣ ∣ d t = ∫ 0 2 π ( ⋅ ) ∣ ∣ ∣ ∣ d t = ∫ 0 2 π ( 9 cos 3 ( t ) + 3 sin 2 ( t ) ) 3 2 sin 2 ( t ) + 3 2 cos 2 ( t ) d t = ∫ 0 2 π ( 9 cos 3 ( t ) + 3 sin 2 ( t ) ) 3 sin 2 ( t ) + cos 2 ( t ) ⏟ = 1 d t = ∫ 0 2 π ( 9 cos 3 ( t ) + 3 sin 2 ( t ) ) 3 d t = 9 ∫ 0 2 π ( 3 cos 3 ( t ) + sin 2 ( t ) ) d t \begin C start color #bc2612, C, end color #bc2612 itself, since that's all you need. Flux integrals of vector fields that can be written as the curl of a vector field are surface independent in the same way that line integrals of vector fields that can be written as the gradient of a scalar function are path independent. Suppose the velocity of a fluid in xyz space is described by the vector field F(x,y,z). Determine whether or not the follow-ing vector elds are conservative. Flux (Surface Integrals of Vectors Fields). Step 3: Simplify the integrand, which involves two vector-valued partial derivatives, a cross product, and a dot product.
Step 2: Apply the formula for a unit normal vector. I even found a specific minute with this problem. Surface Integrals and Flux Problem 1 (Stewart, Exercises 16.5.(13,15,18)). Step 1: Parameterize the surface, and translate this surface integral to a double integral over the parameter space. (ru × rv ) dudv dS F The notation dS.A where S is 2 x² + y² with 0 5 x 5 4,05 y 5 oriented upward. The flux integral of F through S is defined as the double integral RR RR S F (7+2) 0 Question Transcribed Image Text: Calculate the flux integral (7+2). But data is correct when I select that specific hour. the integral of the derivative of Fon S to the integral of F itself on the boundary of S. Calculate the flux integral (7+2) where Sisx²+² with 0 x4.0 sys & oriented upward. Yes, there can be syntax error, it may give you still wrong result, but it is only direction. SELECT integral (value) / 3600000 FROM W WHERE (entityid ‘activeenergyimporttotal’) AND timeFilter GROUP BY time (1h) fill (null) When the selected period is the whole day, there are a few hours with the wrong data. Generic approach - please don’t blame if it doesn’t work for your use case - unfortunately you didn’t provided sampling frequency (assuming 5m), queries are images (I really don’t want OCR that weird measurement name), I don’t have your dataset.


 0 kommentar(er)
0 kommentar(er)
